
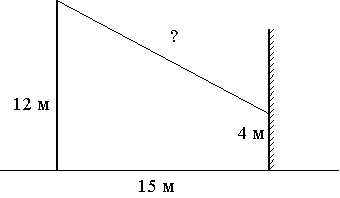
 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
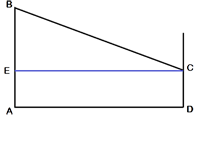 Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD.
Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD.
AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD=15 и EA=CD=4.
Треугольник BCE прямоугольный, тогда
по
теореме Пифагора:
BC2=CE2+EB2
BC2=CE2+(BA-EA)2
BC2=152+(12-4)2
BC2=225+64
BC2=289
BC=17.
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
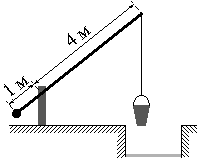 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
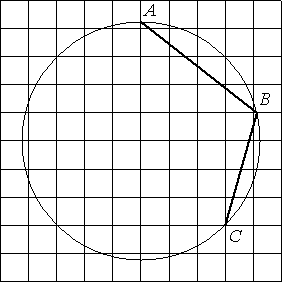 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
 Медиана равностороннего треугольника равна 9√
Медиана равностороннего треугольника равна 9√
Комментарии: