
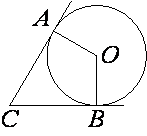 В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Рассмотрим четырехугольник AOBC.
∠C=83° (по условию задачи).
∠CAO=∠CBO=90° (по
первому свойству касательной).
Сумма любого n-угольника равна (n-2)180°, значит сумма углов четырехугольника равна:
(4-2)180°=360°
Т.е. ∠C+∠CAO+∠CBO+∠AOB=360°
83°+90°+90°+∠AOB=360°
∠AOB=360°-83°-90°-90°
∠AOB=97°
Ответ: 97
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
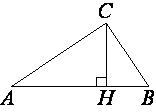 В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
 В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
Комментарии:
(2021-10-27 18:20:41) Лена : центр окружности описанной треуг АВС лежит на стороне АВ Найти Угол АВС если угол ВАС равен 30