
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
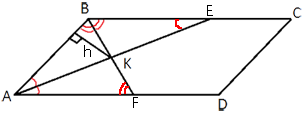 Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
∠FAK=∠BEK (т.к. это
накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по
первому признаку равенства треугольников.
Следовательно и
высоты у этих треугольников тоже равны.
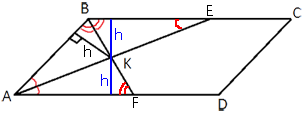 Аналогично, равны и треугольники ABK и AFK.
Аналогично, равны и треугольники ABK и AFK.
Получается, что высота
параллелограмма равна 2h.
Площадь
параллелограмма равна SABCD=2h*BC=2*5*5=50
Ответ: 50
Поделитесь решением
Присоединяйтесь к нам...
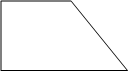 Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
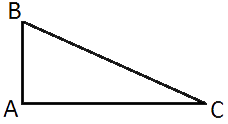 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
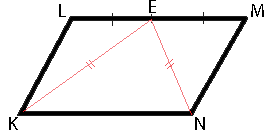 В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
Комментарии:
(2015-10-07 22:45:45) Администратор: Валерий, спасибо за подсказку другого подхода к решению.
(2015-10-07 22:28:15) Валерий: Точки, лежащие на биссектрисах углов равноудалены от сторон этих углов, значит точка К равноудалена от AB, AD и BC, тогда расстояние от точки К до ВС равно расстоянию от точки К до AD и равно расстоянию от точки К до АВ, т.е. равно 5. Тогда высота H к ВС равна 10 и SABCD=H*BC=10*5=50. Ответ: 50. Благодарю авторов за сайт и за ответ.