Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда ∠ADC=46°+35°=81°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=81°+81°+∠DCB+∠CBA,
∠DCB+∠CBA=360°-81°-81°=198°, а учитывая, что ∠DCB=∠CBA (по тому
свойству равнобедренной трапеции), получаем ∠DCB=∠CBA=198°/2=99°, эти углы и есть бОльшие в трапеции
Ответ: 99
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
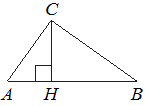На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
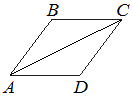В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: