
 Площадь прямоугольного треугольника равна 18√
Площадь прямоугольного треугольника равна 18√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin60°=√
sin60°=a/c=√
c=2a/√
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a/√
a2+b2=4a2/3
3(a2+b2)=4a2
3a2+3b2=4a2
3b2=a2
b2=a2/3
b=a/√
Из условия:
Sтреугольника=ab/2=18√
a*(a/√
a2/√
a2=√
a2=36(√
a2=36
a=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
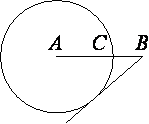 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
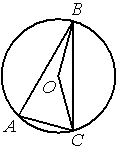 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
 В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
Комментарии: