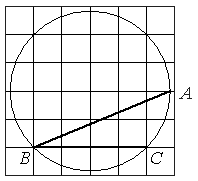
Найдите угол ABC. Ответ дайте в градусах.
Угол ABC (обозначим его α) является
вписанным в окружность, следовательно, он равен половине центрального угла, опирающегося на ту же дугу 2α (по
теореме).
Найдем
центральный угол через тангенс. Рассмотрим
центральный ("синий") угол и проведенный в нем катет ("зеленый").
tg(2α)=2/2=1
По
таблице угол 2α=45°
α=45°/2=22,5°
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
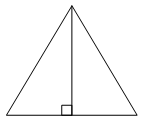Сторона равностороннего треугольника равна 2√
Катеты прямоугольного треугольника равны
√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: