Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Так как треугольник ABC
равнобедренный, то:
∠BAC=∠BCA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠BAC+∠BCA+∠ABC
180°=x+x+79°
101°=2x
x=50,5°=∠BAC
∠BAC -
вписанный в окружность угол, следовательно градусная мера дуги, на которую он опирается (дуга BC) вдвое больше самого угла:
2*50,5°=101°
∠BOC -
центральный угол, следовательно, он равен градусной мере дуги, на которую он опирается, т.е. 101°
Ответ: 101
Поделитесь решением
Присоединяйтесь к нам...
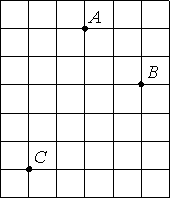На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
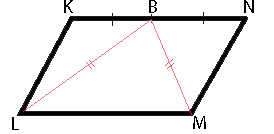В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
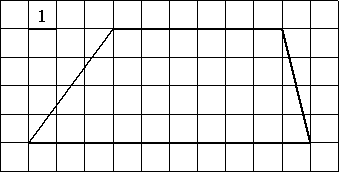Найдите площадь трапеции, изображённой на рисунке.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-21 09:50:57) Дурак: Спасибо, всё правильно.