Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Вариант №1 Предложила пользователь Надя.
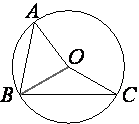Проведем отрезок OB.
Рассмотрим треугольник AOB.
Так как AO=BO (это радиусы окружности), то данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠ABO=39° (по
свойству равнобедренного треугольника)
∠OBC=∠ABC-∠ABO=71°-39°=32°.
Треугольник BOC тоже
равнобедренный, т.к. OB=OC (радиусы окружности).
Следовательно, ∠OBC=∠BCO=32° (по
свойству равнобедренного треугольника).
Ответ: 32
Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).Поделитесь решением
Присоединяйтесь к нам...
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
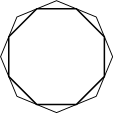Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: