
 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Площадь
трапеции равна произведению высоты на полусумму оснований:
SABCD=h*(BC+AD)/2=h*l, где l -
средняя линия трапеции l=(BC+AD)/2. Следовательно, нам надо найти высоту h.
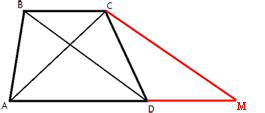 Продлим основание AD и проведем отрезок из вершины C, параллельный BD до пересечения с продленным основанием в точке M (как показано на рисунке).
Продлим основание AD и проведем отрезок из вершины C, параллельный BD до пересечения с продленным основанием в точке M (как показано на рисунке).
В четырехугольнике BCMD сторона CM||BD (мы сами так провели СМ) и DM||BC (по определению
трапеции).
Следовательно, четырехугольник BCMD -
параллелограмм.
Тогда, по
свойству параллелограмма, DM=BC.
AM=AD+DM=AD+BC=2l=2*10=20
Рассмотрим треугольник ACM.
Мы знаем длины всех его сторон, следовательно можем найти площадь через полупериметр:
Полупериметр p=(AC+CM+AM)/2=(AC+BD+AM)/2=(15+7+20)/2=21
SACM=√
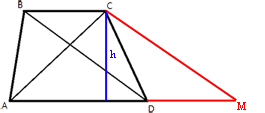 По другой формуле SACM=h*AM/2=42
По другой формуле SACM=h*AM/2=42
h=2*42/AM=2*42/20=4,2
Теперь мы можем вычислить площадь трапеции:
SABCD=h*l=4,2*10=42
Ответ: 42
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
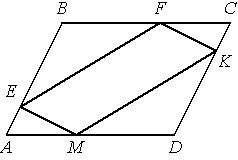 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
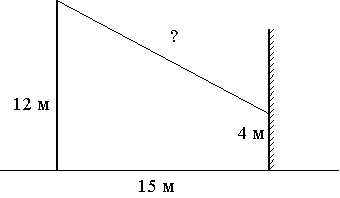 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
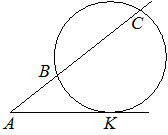 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
 В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
Комментарии:
(2019-04-23 17:16:38) Ваня: Изи