
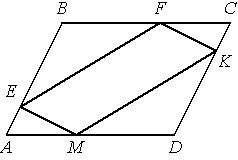
 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Рассмотрим треугольники АЕМ и CKF.
АM = CF (по условию задачи)
∠A=∠C (по
свойству параллелограмма)
Т.к. AB=CD (по
свойству параллелограмма), а BE = DK (по условию), то АE=CK.
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
Аналогично доказывается, что треугольники EBF и KDM тоже равны, следовательно EF=MK.
Т.е. противоположные стороны данного четырехугольника равны. Соответственно этот четырехугольник - параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
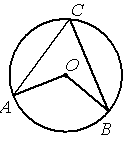 Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
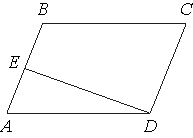 Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
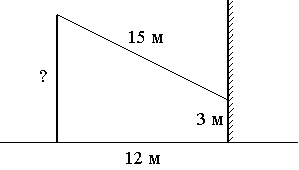 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
 Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Комментарии: