
 Лестница соединяет точки A и B и состоит из 30 ступеней. Высота каждой ступени равна 13 см, а длина – 84 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 30 ступеней. Высота каждой ступени равна 13 см, а длина – 84 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 132+842=169+7056=7225
Тогда длина гипотенузы равна √
Т.к. ступеней 30 шт., то расстояние от А до В составляет 30*85=2550 см, что равняется 25,5 м.
Ответ: 25,5
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
 Площадь прямоугольного треугольника равна 128√
Площадь прямоугольного треугольника равна 128√
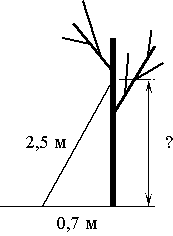 Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
 Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Комментарии: