В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
160°+∠ACB+2x=180°
∠ACB+2x=20°
x=(20°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
169°+∠ACB+x=180°
∠ACB+x=11°
Подставляем значение x, полученное ранее:
∠ACB+(20°-∠ACB)/2=11° |*2
2∠ACB+20°-∠ACB=22°
∠ACB=22°-20°=2°
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
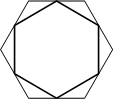Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
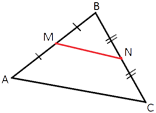Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
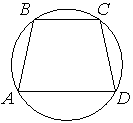Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: