Катеты прямоугольного треугольника равны 4√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=22+(4√
AB2=4+16*6=100
AB=10
Меньший угол лежит напротив меньшей стороны, 2<4√
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
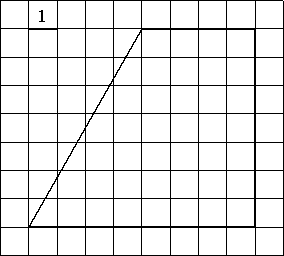Найдите площадь трапеции, изображённой на рисунке.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Найдите площадь параллелограмма, изображённого на рисунке.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: