
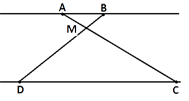 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=12, DC=48, AC=35.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=12, DC=48, AC=35.
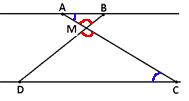 Рассмотрим треугольники ABM и CDM.
Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (так как они
вертикальные).
∠BAM=∠MCD (так как они
внутренние накрест-лежащие).
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, мы можем записать:
DC/AB=MC/AM
48/12=MC/AM
4=MC/AM
4=MC/AM
MC=4AM
AC=AM+MC (по рисунку)
35=AM+4AM
35=5AM
AM=7
MC=4AM=4*7=28
ответ: MC=28
Поделитесь решением
Присоединяйтесь к нам...
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
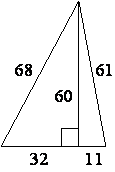 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Комментарии:
(2017-01-23 20:14:14) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-23 08:25:28) : 3Х^3+5х^2-х-5=0
(2017-01-23 08:24:49) : 3Х^3+5х^2-х-5=0