
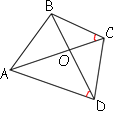
 В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
Вариант 1
∠BCA и ∠BDA опираются на отрез AB и равны друг другу.
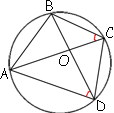 Значит мы можем провести окружность через точки AB и вершины этих углов. Эти углы окажутся
вписанными в окружность, опирающимися на одну дугу.
Значит мы можем провести окружность через точки AB и вершины этих углов. Эти углы окажутся
вписанными в окружность, опирающимися на одну дугу.
Получится, что мы описали окружность вокруг четырехугольника.
Заметим, что углы ABD и ACD тоже являются
вписанными и опирающимися на одну и ту же дугу, т.е., используя
теорему о вписанном угле, получаем, что они равны друг другу .
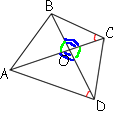 Рассмотрим треугольники OBC и OAD.
Рассмотрим треугольники OBC и OAD.Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
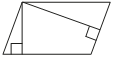 Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
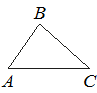
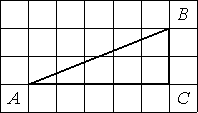 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
 В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
Комментарии:
(2018-04-13 20:04:15) маша: спасибо
(2017-03-09 20:00:07) Администратор: Генрих, пожалуйста, обращайтесь. Кстати, Ваш вопрос очень правильный.
(2017-03-07 17:42:44) Генрих: Да, все грамотно) спасибо большое)
(2017-03-06 22:58:18) Администратор: Генрих, можно доказать от обратного. Например, эти два угла являются вписанными для разных окружностей. Но при этом градусные меры дуг совпадают, так как вписанные углы равны. Следовательно, и радиусы у этих окружностей равны. Таких окружностей можно провести только две, и только так, чтобы ценры окружностей располагались по разные стороны от нашей хорды. А в нашем случае центры явно лежат по одну сторону. Получается, что окружности совпадают, т.е. углы принажлежат одной окружности.
(2017-03-03 17:13:03) Генрих: Скажите пожалуйста, как доказать, что если два угла, в данном случае BDA BCA, опираются на одну дугу и равны, то они вписаны в одну и ту же окружность? По-моему это не очевидно.
(2016-12-21 18:50:49) Инна: Да. Класс! Теперь понятно, что методом преобразования из первой пропорции получается вторая. Большое спасибо.
(2016-12-20 17:00:17) Администратор: Инна, теперь я Вас понял. Я добавил в решение пару строк, чтобы все стало правильно и понятно. Я, видимо, зря опустил эти вычисления. Спасибо, что обратили на это внимание. Теперь все хорошо?
(2016-12-20 16:34:00) Инна: То есть я пишу о доказательстве подобия треугольников АВО и ДСО, где используется второй признак подобия. Из полученной пропорции нельзя сделать вывод, что стороны треугольников АВО и ДСО пропорциональны.
(2016-12-20 16:27:01) Инна: Речь идёт о втором признаке, когда доказывается подобие второй пары треугольников на основании полученной пропорции.И тут и не получается того, что стороны пропорциональны.
(2016-12-20 11:41:03) Администратор: Инна, по первому признаку подобия треугольников. "Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны". А уже из доказанного подобия мы можем утверждать о пропорциональности сторон.
Нажимайте на ссылки в решении, тогда вы увидите материалы на которые я ссылаюсь.
(2016-12-19 19:50:21) Инна: Во втором варианте отношения сторон ОВ и ОА, а также ОС и ОД разве можно назвать отношениями пропорциональных сторон треугольников АВО и ВСО? Мы же видим, что ОВ и ОА - стороны одного треуг.АВО, так же и стороны ОС и ОД - стороны одного треуг.ВСО? Каким образом приведённое в задаче отношение доказывает пропорциональность сторон треугольников АВО и ВСО?
(2016-12-17 10:33:42) Администратор: Владислав, тут тонкий момент. Пусть АВ - это хорда какой-то окружности (мы пока не знаем как она проходит). Таких окружностей бесконечно много. Выберем такую окружность, для которой угол BCA будет вписанным.Через точки A, B и C всегда можно провести окружность. А так как угол BDA равен BCA и опирается на ту жу дугу, то угол BDA тоже окажется вписанным в окружность. Таким образом получится, что окружность описана вогруг четырехугольника.
(2016-12-16 14:04:00) Владислав: Да, я тоже не понимаю кто сказал что мы можем описать окружность, надо сначала доказать что сумма противоположных углов 180.
(2016-05-29 12:27:41) Администратор: Елена, Вертикальные углы - это углы образованные двумя пересеченными прямыми и находящиеся напротив друг друга. Параллельные прямые тут вообще ни при чем.
(2016-05-29 11:52:54) Елена: Вопрос по 2 варианту решения. Как углы BOC и AOD могут быть вертикальными, если мы не знаем, что ВС параллельна AD?
(2015-04-30 20:46:35) Администратор: Саша, ни в условии, ни в решении нет ни одного слова про трапецию.
(2015-04-30 18:53:49) Саша: А разве можно просто так взять и описать окружность около трапеции. Ведь чтобы описать нужно равнобокую трапецию?