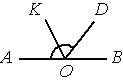
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
∠AOD=180°-∠DOB=180°-64°=116° (так как ∠AOB - развернутый, т.е. равен 180°).
Так как OK - биссектриса, то ∠DOK=∠AOD/2=116°/2=58°
Ответ: 58
Поделитесь решением
Присоединяйтесь к нам...
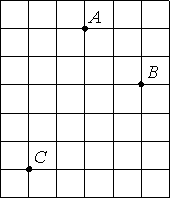На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
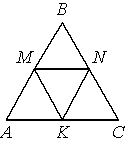В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Лестница соединяет точки A и B и состоит из 30 ступеней. Высота каждой ступени равна 13 см, а длина – 84 см. Найдите расстояние между точками A и B (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: