
 В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=16
По
определению средней линии трапеции: m=(BC+AD)/2=16/2=8
Ответ: m=8
Поделитесь решением
Присоединяйтесь к нам...
 На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
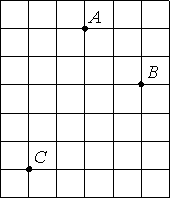 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
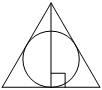 Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
 Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
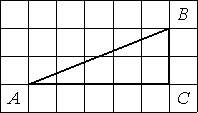 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Комментарии: