Найдите площадь треугольника, изображённого на рисунке.
Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
582=AC2+422
AC2=3364-1764=1600
AC=40
SABC=40*42/2=20*42=840
Ответ: SABC=840
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
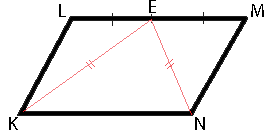В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: