Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
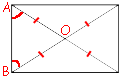
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO -
равнобедренный.
По первому
свойству равнобедренного треугольника:
∠OBA=∠OAB
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+75°+75°
∠AOB=30°
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: