
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
∠CBA - является
смежным внешнему углу, следовательно, 180°=∠CBA+155°
∠CBA=180°-155°=25°
Так как AC=BC, то треугольник ABC -
равнобедренный.
Значит ∠CBA=∠CAB=25° (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=25°+25°+∠C
∠C=130°
Ответ: 130
Поделитесь решением
Присоединяйтесь к нам...
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
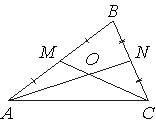 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=18. Найдите CO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=18. Найдите CO.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Комментарии: