В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Продлим стороны AB и CD до пересечения друг с другом.
Рассмотрим треугольник AED.
По
теореме о сумме углов треугольника:
180°=∠EDA+∠DAE+∠AED
180°=90°+∠AED
∠AED=90°
Следовательно треугольник AED -
прямоугольный.
Рассмотрим треугольники AED и BEC.
∠AED - общий
∠EBC=∠EAD (т.к. это
соответственные углы)
Треугольники AED и BEC
подобны (по
первому признаку подобия треугольников).
Тогда по
определению подобия:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
49/21=(20+BE)/BE
49BE/21=20+BE
28BE/21=20
BE=20*21/28=15
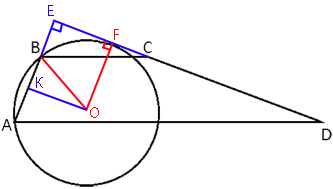Обозначим точку F - точку касания прямой CD и окружности.
OF - искомый радиус окружности. Он перпендикулярен касательной EC (по
свойству касательной).
Проведем отрезок ОК перпендикулярно АВ.
OK - серединный перпендикуляр к
хорде AB (
третье свойство хорды)
Получается, что BK=AB/2=20/2=10.
EK=BE+BK=15+10=25
EK=OF=R=25, так как OKEF - прямоугольник.
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 150°, AB=4. Найдите радиус окружности, описанной около этого треугольника.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
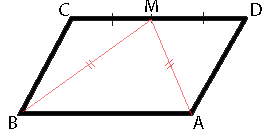В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
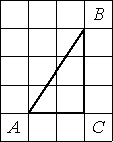Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-01-19 21:22:57) Администратор: Евгений Бакин, согласен с Вами. Решение упрощено по Вашему варианту.
(2017-12-29 11:41:46) Евгений Бакин: Проще найти сразу OF=EK=EB+BK=15+10=25