Автор: Таська
В треугольнике ABC проведена биссектриса AL, угол ALC равен 148°, угол ABC равен 132°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
132°+∠ACB+2x=180°
∠ACB+2x=48°
x=(48°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
148°+∠ACB+x=180°
∠ACB+x=32°
Подставляем значение x, полученное ранее:
∠ACB+(48°-∠ACB)/2=32° |*2
2∠ACB+48°-∠ACB=64°
∠ACB=64°-48°=16°
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Площадь прямоугольного треугольника равна 800√
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
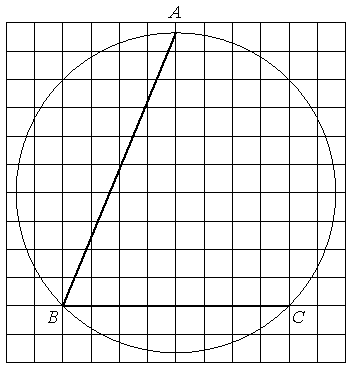Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
В треугольнике ABC угол C равен 45°, AB=6√
Хочу получать новые решения
Ни какого спама
Комментарии:
(2015-03-25 01:19:26) Lora: Другое решение.Угол ALB=32 180-148 смежные углы. Тогда угол BAL 180-132-32=16. Угол LAC = 16, т.к. AL биссектриса. Тогда получаем, что угол ACB равен 180-148-16=16.