
 В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Рассмотрим треугольники AA1B и CC1B.
∠ABA1=∠CBC1, так как они
вертикальные.
∠AA1B=∠CC1B, так как они прямые по условию задачи.
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, по
определению подобных треугольников:
AB/BC=A1B/C1B
Преобразуем это равенство:
AB/A1B=BC/C1B
Рассмотрим треугольники A1BC1 и ABC.
∠ABC=∠A1BC1, так как они
вертикальные.
Тогда, по
второму признаку подобия, данные треугольники
подобны.
Поделитесь решением
Присоединяйтесь к нам...
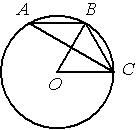 Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
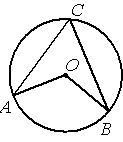 Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
 Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Комментарии:
(2014-11-27 18:14:34) Любовь: Спасибо за помощь и за создание такого прекрасного сайта.