Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Рассмотрим каждое утверждение:
1) "Против большей стороны треугольника лежит больший угол" - это утверждение верно, по
теореме о соотношениях между сторонами и углами треугольника.
2) "Любой прямоугольник можно вписать в окружность" - это утверждение верно, так как, чтобы четырехугольник можно было вписать в окружность, должно выполняться условие - сумма противолежащих углов четырехугольника должна равняться 180°. Для Прямоугольника это условие выполняется.
3) "Площадь треугольника меньше произведения двух его сторон". Площадь треугольника можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
Ответ: 1), 2), 3)
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Стороны AC, AB, BC треугольника ABC равны 2√
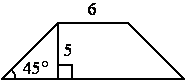В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Найдите площадь параллелограмма, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: