
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
 ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=17/19 (по первому
свойству биссектрисы).
Из этих равенств выписываем:
AD=CD*17/19
BD=CD*19/17, (BD=AD+AB=AD+19+17=AD+36)
AD+36=CD*19/17
CD*17/19+36=CD*19/17
36=CD*(19/17-17/19)
36=CD*((19*19-17*17)/(17*19))
36=CD*(361-289)/323
36*323=CD*72
CD=161,5
Ответ: CD=161,5
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
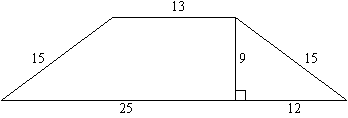 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
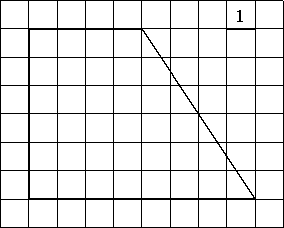 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
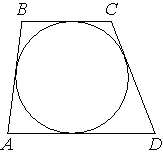 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Комментарии:
(2015-01-11 19:03:10) Маргарита: Огромное спасибо за помощь.