
 Площадь прямоугольного треугольника равна 2450√
Площадь прямоугольного треугольника равна 2450√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=2450√
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√
BC=AC√
S=AC*BC/2=2450√
AC*BC=4900√
AC*AC√
AC2=4900
AC=70
Ответ: 70
Поделитесь решением
Присоединяйтесь к нам...
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
 В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
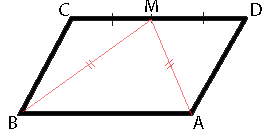 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
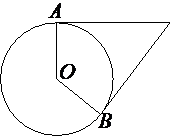 Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Комментарии: