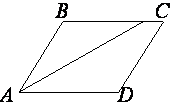Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
∠BCA=∠DAC=1° (т.к. это
накрест-лежащие углы)
А так как AC -
биссектриса, то ∠BAC=∠DAC=1°.
∠A=∠BAC+∠DAC=1°+1°=2°
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Синус острого угла A треугольника ABC равен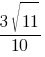 
. Найдите CosA.
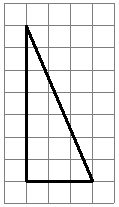На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: