Автор: Алла
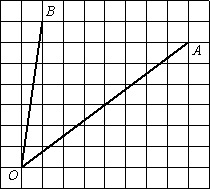
Найдите тангенс угла AOB.
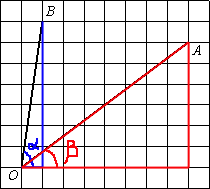Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.
1) Для синего треугольника: tgα=7/1=7
2) Для красного треугольника: tgβ=6/8=0,75
Есть тригонометрическая формула:
tg(α-β)=(tgα-tgβ)/(1+tgα*tgβ)
Вычисляем:
tg∠AOB=tg(α-β)=
(7-0,75)/(1+7*0,75)=6,25/6,25=1
Ответ: tg∠AOB=1
Поделитесь решением
Присоединяйтесь к нам...
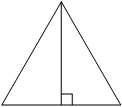Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Хочу получать новые решения
Ни какого спама
Комментарии:
(2016-03-13 23:51:56) Администратор: Вера, хороший подход к решению задачи, а радиус векторы входят в программу 9-го класса?
(2016-03-11 15:57:48) Вера: Введем координатную плоскость, начало координат вершина угла.Радиус вектор ОВ(1;7); радиус векторОА(4;3). Находим соsОАВ=(ОА*ОВ)/(!ОА!*!ОВ!).Где ОА*ОВ-Скалярное произведение=25;!ОА!=5; !ОВ!=кв корень из50-длины векторов.соsОАВ=1/кв корень из2. УголОАВ=45,значит тангенс ОАВ=1
(2014-05-29 07:11:44) Софья: Спасибо
(2014-05-28 08:29:06) Администратор: Софья, не могу знать. Успехов на экзамене!
(2014-05-28 07:43:07) Софья: Ладно. Спасибо! Настоящая работа ГИА будет сложнее?
(2014-05-27 15:13:13) Администратор: София, конечно может встретиться, так как условие задачи взято с сайта fipi.ru, откуда и будут набираться задачи на экзамен.
(2014-05-27 08:30:24) Софья: Такие задачи встречаются в экзамене?
(2014-05-23 14:39:30) Марина: Да, все получается
(2014-05-23 14:25:06) Администратор: Эля, я, оказывается, не понял, какие стороны треугольника равны. В данной задаче, действительно можно решить как Вы предлагаете. Но это решение не универсально. Без формулы решить можно как предложил пользователь Евгений (через теорему косинусов). Такое решение описано в задаче 482.
(2014-05-23 12:08:59) Эля: И еще,если соединить В с серединой ОА,тоже получатся равные катеты равные 5.
(2014-05-23 11:12:35) Эля: А по клеточкам если посчитать,сторона ВА равна ОВ,все получится и не развалится.
(2014-05-23 08:37:50) Администратор: Если соединить A и B мы не получим равнобедренный треугольник. Можете проверить по теореме Пифагора. Стороны разные. Поэтому разваливается все Ваше решение.
(2014-05-23 01:03:35) : Можно обойтись без формулы. 1.Соединить В и А,получим равнобедренный треугольник 2.По Пифагору найдем все его стороны. 3.Опустим из В высоту-медиану ВК,найдем ее величину и увидим ,что она равна катету СК. 4.Катеты равны ,все счастливы.
(2014-05-14 19:47:36) Администратор: Марина, этого я объяснить не могу, так как такой информации у меня нет. Я с Вами полностью согласен, мне попадались и другие задачи, которые решаются очень легко только с тригонометрическими формулами, а без них, решать приходилось вычисляя 5-значные числа.
(2014-05-14 14:41:13) Марина: Скажите, пожалуйста, почему в экзамен 9 класса включено задание, подразумевающее знание формул тригонометрии, которую проходят только в 10 классе?