Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
SO=VO (т.к. это радиусы окружности)
SO=VO=ST=TV (по
определению ромба)
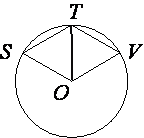Проведем отрезок OT.
OT тоже радиус окружности, следовательно OT=SO=VO=ST=TV
Следовательно, треугольники STO и TVO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно и ∠OVT=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь трапеции, изображённой на рисунке.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: