В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=55°
Ответ: /OCD=55°.
Поделитесь решением
Присоединяйтесь к нам...
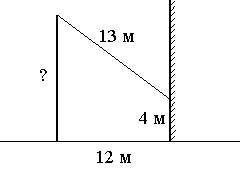От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-14 20:09:10) Администратор: Катя, была проблема у хостера, проблема устранена. Сейчас все читаемо?
(2017-02-14 14:50:46) Катя: не грузит решение, все в знаках вопроса. что такое??