В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
∠QNM - является
вписанным в окружность и опирается на дугу QM.
∠QPM тоже является
вписанным в окружность и опирается на дугу QM.
Следовательно, эти углы равны.
∠QNM=∠QPM
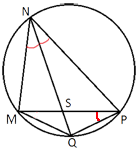Рассмотрим треугольники NPQ и SPQ.
∠SQP - общий
∠QNP=∠SPQ
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, NQ/QP=QP/SQ
NQ=QP2/SQ=862/43=88=7396/43=172
NS=NQ-SQ=172-43=129
Ответ: NS=129
Поделитесь решением
Присоединяйтесь к нам...
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника три оси симметрии.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
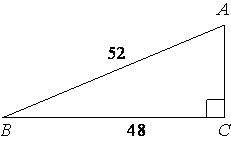Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-04 20:09:35) Администратор: NQ/QP=QP/SQ => NQ=QP*QP/SQ=QP^2/SQ
(2017-05-04 16:56:15) : почему в квадрате?
(2015-03-09 17:03:15) Рина: спасибо за красивое решение