Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Площадь любого треугольника равна половине произведения
высоты и стороны, к которой
высота проведена.
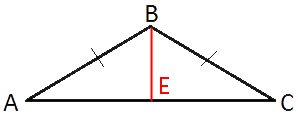
Проведем
высоту как показано на рисунке.
По
свойству равнобедренного треугольника BE - и
высота, и
медиана. Следовательно, AE=EC=AC/2.
Треугольник ABE -
прямоугольный (т.к. BE -
высота).
По
теореме Пифагора найдем высоту BE:
AB2=AE2+BE2
AB2=(AC/2)2+BE2
342=(60/2)2+BE2
1156=900+BE2
BE2=256
BE=16
SABC=(BE*AC)/2=(16*60)/2=16*30=480
Ответ: SABC=480
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
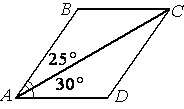Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-28 22:37:16) Администратор: Павел, правильно заданный вопрос - это половина правильного ответа )))
(2014-05-28 21:36:02) Павел: Только написал и сразу понял
(2014-05-28 21:35:07) Павел: Откуда в 4 строчке 900?