
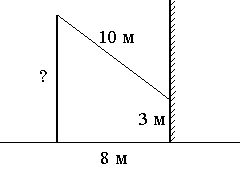
 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
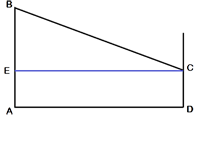 Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
По
теореме Пифагора BC2=CE2+EB2
102=82+EB2
EB2=100-64
EB2=36
EB=6.
Высота столба = EB+EA=6+3=9.
Ответ: Высота столба - 9 метров.
Поделитесь решением
Присоединяйтесь к нам...
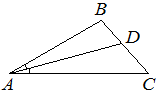 В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
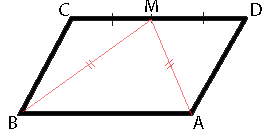 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Комментарии: