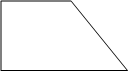
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Введем обозначения и проведем
высоту BE, перпендикулярный CD как показано на рисунке.
По условию AB=BE=40
Тогда ABED -
квадрат (все углы прямые и все стороны равны).
Треугольник BCE -
прямоугольный, следовательно,
по
определению tgC=BE/EC=5/3.
40/EC=5/3 => EC=40*3/5=24
DC=DE+EC
DE=AB (по
определению квадрата)
DC=40+24=64
Ответ: DC=64
Поделитесь решением
Присоединяйтесь к нам...
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике ABC AC=15, BC=5√
Радиус окружности, описанной около квадрата, равен 16√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-02-11 16:42:46) Игорь : В треугольнике ABC, AC=13 см и биссектриса угла A делит сторону BC на отрезки BM=3см, MC=5см. Определите сторону AB.
(2017-02-14 19:13:05) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-02-13 13:14:24) : В трапеции меньшие основание равно √3 дм, а высота-9 дм .Острые углы трапеции равны 60 и 45.Найдите большое основание .
(2016-10-31 21:50:36) Администратор: дина, Ваша задача есть на нашем сайте, ее номер 796.
(2016-10-30 13:49:44) дина: Биссектрисы углов А и В параллелограмма АВСD пересекаются в точке Е. Найдите площадь параллелограмма, если ВС = 12 см , а расстояние от точки Е до стороны АВ равно 9 см