
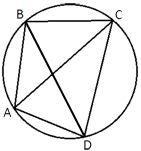 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
∠CAD является
вписанным углом и опирается на дугу CD.
∠CBD тоже
вписанный и тоже опирается на ту же дугу CD, следовательно:
∠CAD=∠CBD=60°
∠ABD=∠ABC-∠CBD=92°-60°=32°
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
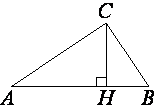 В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
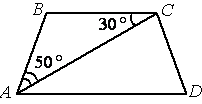 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
Комментарии:
(2016-12-22 20:34:56) Администратор: Андрей, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-22 16:48:54) Андрей: четырехугольник BCDE вписан в окружность.расстояние между точками E и C равно 25, между D и C -7, между D и E -24. найти а) косинус угла CBD; б) BC, если косинус угла BCD=1/5