
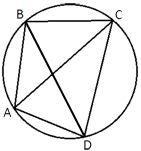 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
∠CAD является
вписанным углом и опирается на дугу CD.
∠CBD тоже
вписанный и тоже опирается на ту же дугу CD, следовательно:
∠CAD=∠CBD=60°
∠ABD=∠ABC-∠CBD=92°-60°=32°
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
 Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Комментарии:
(2016-12-22 20:34:56) Администратор: Андрей, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-22 16:48:54) Андрей: четырехугольник BCDE вписан в окружность.расстояние между точками E и C равно 25, между D и C -7, между D и E -24. найти а) косинус угла CBD; б) BC, если косинус угла BCD=1/5