В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Вариант №1 Предложил пользователь Гоша.
Очевидно, что угол OAB это угол DAB, а ∠DAB является вписанным и опирается на дугу BD.
∠OCD тоже является вписанным и опирается на дугу BD.
Тогда, по теореме о вписанном угле, эти углы равны:
∠OCD=∠OAB=70°.
Ответ: 70
Вариант №2
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника ∠OAB=∠OBA.
Рассмотрим треугольники АОВ и COD. ∠DOC=∠AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по первому признаку). Поэтому ∠OBA=∠OAB=∠ODC=∠OCD=70°
Ответ: 70
Поделитесь решением
Присоединяйтесь к нам...
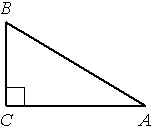В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
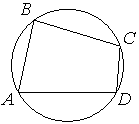Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Косинус острого угла А треугольника равен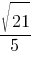 
. Найдите sinA.
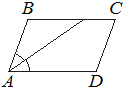Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-06-03 21:42:10) Администратор: Гоша, да, действительно. Элегантно и просто. Обязательно скоро размещу такое решение под Вашим именем. Спасибо!
(2019-06-03 12:10:28) гоша: А разве нельзя сразу заключить, что этот угол равен 70 градусам, так как опирается на ту же дугу что и данный угол