
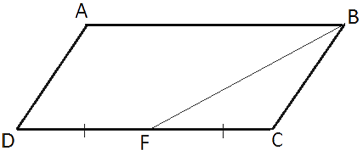 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
BC=CD/2=CF (по условию задачи)
Следовательно треугольник BCF -
равнобедренный.
По
свойству равнобедренного треугольника:
∠CFB=∠CBF
∠CFB=∠ABF (так как это
накрест-лежащие углы)
Получается, что ∠CBF=∠ABF
Следовательно, BF -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
 Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
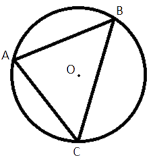 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
 Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
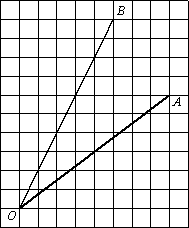 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Комментарии:
(2022-09-12 10:35:22) : АВ = CD = 14 см, ВС = AD = 27 см за властивостями параллелограмма Р ABCD = АВ + CD + ВС + AD Р ABCD = … Відповідь :