Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Так как AC проходит через центр окружности, значит это диаметр.
Треугольник ABC вписан в окружность и центр окружности лежит на середине AC, следовательно треугольник ABC
прямоугольный с гипотенузой AC(по
теореме об описанной окружности).
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=30°+90°+∠C
∠C=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
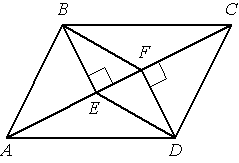В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 21:48:02) Алина: Потому что ∠ABC прямоугольный =90°
(2014-05-26 18:48:07) мариша: Откуда взяли 90°?
(2014-05-19 13:03:26) ольга: можно еще через дуги. дуга bc=60 т.к. ac диаметр ,то 360:2=180 значит дуга ab=120 и т.к. <с=1/2 дуги ab, то <с=60
(2014-05-18 12:58:49) Ирина: все понятно спасибо