
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 64°*2=128°.
Тогда дуга NB равна 180°-128°=52°
/NMB - тоже
вписанный в окружность, следовательно он равен 52°/2=26°
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
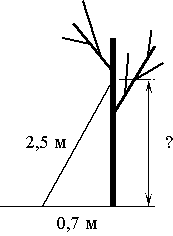 Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
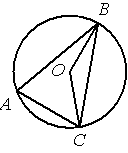 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
 Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
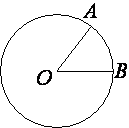 На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
Комментарии: