ОГЭ, Математика.
Геометрия: Задача №077612
| Задача №399 из 1087
Условие задачи: | |
 Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Решение задачи:
Вариант №1
AB -
гипотенуза, BC - катет.
Найдем AC по
теореме Пифагора:
AB2=BC2+CA2
392=152+CA2
1521=225+CA2
1296=CA2
CA=36
Для треугольника ABC:
sinA=CB/AB=15/39=5/13
Для треугольника ACD:
sinA=CD/AC => CD=AC*sinA=36*5/13=180/13=13 целых и 11/13
Ответ: СD=13 целых и 11/13
Вариант №2 (предложил Даниил)
AB -
гипотенуза, BC - катет.
Найдем AC по
теореме Пифагора:
AB
2=BC
2+CA
2
39
2=15
2+CA
2
1521=225+CA
2
1296=CA
2
CA=36
Площадь любого треугольника равна половине произведения высоты на сторону, к которой высота проведена, т.е. S=(a*h)/2.
S
ABC=(AB*CD)/2
Так же площадь треугольника, если треугольник прямоугольный, можно найти по формуле: половина произведения катетов.
S
ABC=(AC*BC)/2
Так как это площади одного и того же треугольника, то:
(AB*CD)/2=(AC*BC)/2
AB*CD=AC*BC
39*CD=36*15
CD=36*15/39=36*5/13=180/13=13 целых и 11/13
Ответ: 13 целых и 11/13
Вы можете поблагодарить автора, написать свои претензии или предложения на
странице 'Про нас'
Другие задачи из этого раздела
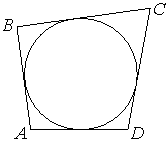 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
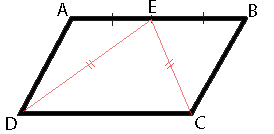 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Стороны AC, AB, BC треугольника ABC равны 3√2, √14 и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если /KAC>90°.

 Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе. Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник. Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке. Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Комментарии:
(2016-04-13 14:40:14) Администратор: Даниил, Ваш вариант решения добавлен на наш сайт, спасибо Вам за решение.
(2016-04-12 23:33:56) Администратор: Даниил, обязательно рассмотрю Ваше решение.
(2016-04-10 21:48:56) Даниил: 2 вариант (мой взгляд) AB - гипотенуза, BC - катет. Найдем AC по теореме Пифагора: AB2=BC2+CA2 392=152+CA2 1521=225+CA2 1296=CA2 CA=36 S треугольника=AC*CB/2 (для прямоугольного тр) S треугольника=AB*CD/2 (т.к. CD-высота) значит AB*CD/2=AC*CB/2 39*CD=15*36 (2-ки сокращаются) CD=540/39 (15*36=540) CD=13 и 11/13