
Площадь прямоугольного треугольника равна
338√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin60°=√
sin60°=a/c=√
c=2a/√
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a/√
a2+b2=4a2/3
3(a2+b2)=4a2
3a2+3b2=4a2
3b2=a2
b2=a2/3
b=a/√
Из условия: Sтреугольника=ab/2=338√
a*(a/√
a2/√
a2=√
a2=676(√
a2=676
a=26
Ответ: a=26
Поделитесь решением
Присоединяйтесь к нам...
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
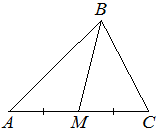 В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
 Медиана равностороннего треугольника равна 9√
Медиана равностороннего треугольника равна 9√
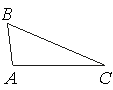 В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
 Площадь прямоугольного треугольника равна 200√
Площадь прямоугольного треугольника равна 200√
Комментарии: