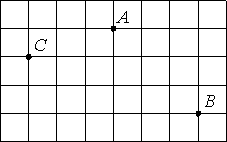
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Площадь клетки равна 1, значит клетка имеет и единичные стороны, т.е. равные 1 (1*1=1).
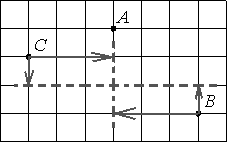Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 3 клетки вправо и на одну клетку вниз.
Относительно точки В на 3 клетки влево и на одну клетку вверх.
Тогда очевидно, что расстояние от точки А до середины ВС равно 2
Ответ: расстояние от точки A до середины отрезка BC равно 2
Поделитесь решением
Присоединяйтесь к нам...
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
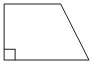Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
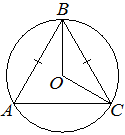Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: