В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Вариант №1
MN -
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
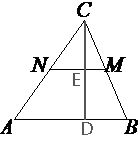Проведем
высоту из вершины С.
SCNM=1/2*CE*NM=57 (по условию).
CE*NM=114
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE -
средняя линия для треугольника ACD, значит CE=ED.
ABMN - трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*114=171
Ответ: SABMN=171
MN -
средняя линия треугольника ABC, по теореме о средней линии MN=AF=FB.Поделитесь решением
Присоединяйтесь к нам...
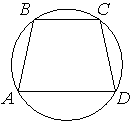Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
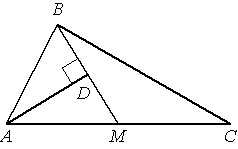Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-28 22:29:42) Администратор: Оксана, по теореме о средней линии треугольника. Нажимайте на ссылки в решении, чтобы посмотреть теоремы, на которые я ссылаюсь.
(2017-02-28 21:56:28) Оксана : Извините , я не очень поняла по первой задаче : почему СЕ = ED ?
(2015-05-26 16:56:28) Денис: Поддержу артема! в АNMB есть 3 одинкаковых треугольника которые равны СNM! просто симметрично относительно NM отложите CNM!
(2015-05-11 18:15:48) Катерина: По моему мнению, возможно второе и более краткое решение. Треугольники CNM ACB подобны по двум углам. Коэффициент подобия равен двум, тк NM средняя линия и равна половине AB. Отношение площадей подобных треугольников равно квадрату коэффициенту подобия, то есть 4. Значит площадь ACB 4*57=228. Площади аддитивны, значит площадь ABMN= площадь ACB - площадь CNM= 228-57=171
(2015-05-11 16:54:23) Катерина: По моему мнению, возможно второе и более краткое решение. Треугольники CNM ACB подобны по двум углам. Коэффициент подобия равен двум, тк NM средняя линия и равна половине AB. Отношение площадей подобных треугольников равно квадрату коэффициенту подобия, то есть 4. Значит площадь ACB 4*57=228. Площади аддитивны, значит площадь ABMN= площадь ACB - площадь CNM= 228-57=171
(2015-04-15 16:11:36) Артём: Из 1 части, обычно 12 задание. Кстати, четырёхугольник ABMN можно разбить на 3 равных треугольника (они будут равны треугольнику CNM). Таким образом 57+57+57=171.
(2015-04-03 20:42:14) Администратор: Марина, точной информации у меня нет, но думаю, что из второй, хотя задача довольно легкая.
(2015-04-03 19:33:34) марина : Эта задача из второй части?