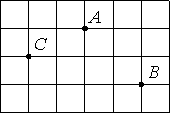
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Площадь клетки равна 1, значит клетка имеет и единичные стороны, т.е. равные 1 (1*1=1).
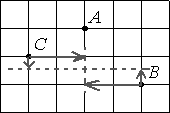Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 2 клетки вправо и на пол клетки вниз.
Относительно точки В на две клетки влево и на пол клетки вверх.
Тогда очевидно, что расстояние от точки А до середины ВС равно 1,5
Ответ: расстояние от точки A до середины отрезка BC равно 1,5
Поделитесь решением
Присоединяйтесь к нам...
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
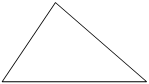В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
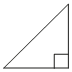В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: