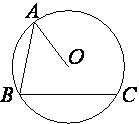
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Проведем отрезки CO и продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Рассмотрим треугольник ABE. По
теореме о сумме углов треугольника запишем:
180°=∠OAB+∠ABC+∠BEA
180°=13°+43°+∠BEA
∠BEA=180°-13°-43°=124°
Смежный этому углу ∠OEC=180°-∠BEA=180°-124°=56° (запомним это)
Угол ABC является
вписанным углом, следовательно градусная мера дуги, на которую он опирается, вдвое больше (по
теореме о вписанном угле), т.е. градусная мера дуги AC равна 43°*2=86°
Угол АОС является
центральным и, соответственно, равен градусной мере дуги, на которую опирается. А опирается он на дугу AC, следовательно ∠AOC=86°
Смежный этому углу ∠COE=180°-∠AOC=180°-86°=94°
Рассмотрим треугольник OCE.
По
теореме о сумме углов треугольника запишем:
180°=∠OEC+∠COE+∠OCE
Вспомнив то, что запомнили ранее...
180°=56°+94°+∠OCE
∠OCE=180°-56°-94°=30°
∠OCE и есть искомый угол BCO.
Ответ: ∠BCO=30°
Поделитесь решением
Присоединяйтесь к нам...
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: