
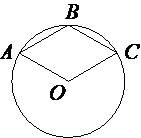 Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
AO=CO (т.к. это радиусы окружности)
AO=CO=AB=BC (по
определению ромба)
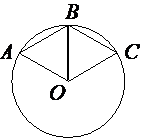 Проведем отрезок OB.
Проведем отрезок OB.
OB тоже радиус окружности, следовательно OB=AO=CO=AB=BC
Следовательно, треугольники ABO и BCO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
/ABC=/ABO+/CBO=60°+60°=120°
Ответ: /ABC=120°
Поделитесь решением
Присоединяйтесь к нам...
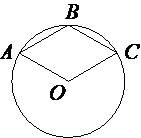 Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
 Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Комментарии: