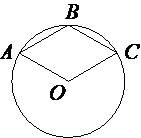Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
AO=CO (т.к. это радиусы окружности)
AO=CO=AB=BC (по
определению ромба)
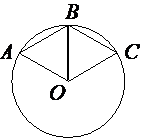Проведем отрезок OB.
OB тоже радиус окружности, следовательно OB=AO=CO=AB=BC
Следовательно, треугольники ABO и BCO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
/ABC=/ABO+/CBO=60°+60°=120°
Ответ: /ABC=120°
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
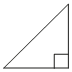В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
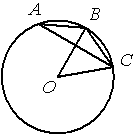Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: