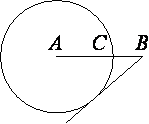На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
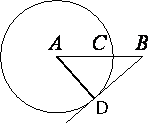Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=75 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(75+10)2=752+BD2
7225=5625+BD2
BD2=1600
BD=40
Ответ: длина касательной равна 40.
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: