На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
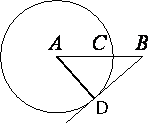Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=75 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(75+10)2=752+BD2
7225=5625+BD2
BD2=1600
BD=40
Ответ: длина касательной равна 40.
Поделитесь решением
Присоединяйтесь к нам...
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: